最短ルートを探せる”A* パスファインディング”を試してみた
こんにちは。開発担当のマットです。
Sploutでは様々なテクノロジーを使って色々開発していますが、その中でも特にゲーム・プログラミングが1番好きです。
日本ではあまり知られていませんが、小さい時からシヴィライゼーションというゲームが大好きでした。
ルールは複雑ですが、目的は単純です。
国のリーダーとして、都市を設立して、軍隊を作り、敵を倒し、世界の征服者になることです。
プログラムを書けるようになった頃、このようなゲームを作成することをすぐ試してみました。
1人の人間のプレーヤー対複数のコンピュータ・プレーヤーのゲームにするつもりだったので、世界のマップを作って将棋盤のようにそれをマスに分けて(海のマス、森林のマス、野原のマス、山のマス、など)、将棋の駒のような軍隊のピースを設置しました。
歩兵部隊、戦車、軍艦など、いろいろな種類を用意して通過可能と通過不可能のマスも定義しました。
歩兵部隊の場合、海と山が通過できない。
戦車の場合、それプラス森林もダメ。
軍艦は海のみ通過できるなど。
一マスずつ動かす場合、コードはとてもシンプルでした。
隣のマスはその駒にとって通過可能であれば、通過を許す。
一マスずつしか動かないので、遠い目的地までのルートは頭の中で管理していました。
ところがコンピュータの番になると目的地までのルート管理で困りました。
駒と目的地の間に山や海やそのような通過不可能なマスがあったら、その障害を避ける方法を見つけなければなりませんが、実際にどうやってするのでしょう?
「パスファインディング」とは?
名前の通り、「パスファインディング」は「パス(道)ファインディング(探し)」のことです。
つまり、「パスファインディング」は A という出発地から B という目的地までの道を見つける方式のこと。
様々なパスファインディング方法がありますが、この記事で紹介するのは1番多く使われている「A* パスファインディング」という方式です。
A* パスファインディング方式の実例
単純に、A*(エイ・スター)とも呼ばれますが、この方式を正しく使うと、必ず1番短い道を見つけることができます。
少し複雑なので、実際の例で説明したいと思います。
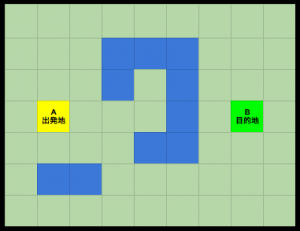
この実例で、このマップのA出発池からB目的地までの一番短い道を探します。
コーディングを始める前には、以下の基本知識が必要となります。
1.パスファインディングの用語で「マス」は「ノード」と言うので、以下では「ノード」と呼ぶ。
2.この実例では、1ノード=1m(メートル)。即ち、上下左右を動く場合、距離は 1.0mとなる。
3.しかし、斜めに行く場合、「√2.0m」となります。実際にそれを使うと処理が遅くなる上、実例が複雑になりますので、端数を切り捨てて、1.4mとする。
4.それぞれのノードは以下の変数を持つ。
> g (これは「今まで辿ってきた道の距離」を持つ変数)
> h (これは「直線で目的地までの距離」を持つ変数)
> p (これは「このノードに着くまでの手前のノード」を指す変数)
5.確認できるノードを「open」というリストに保管する。
6.既に確認したノードは「closed」というリストに保管される。
> 一旦closedに入ると、openに戻されることはない。
7.その時、調べているノードは「current」とされる
A*パスファインディングの手順
1.まず、A出発地を「current」と指定する。
2.currentが目的地であれば終了。
3.以下の条件を満たす場合、currentに接触しているノードをopenリストに追加する。
〈条件〉
接触しているノードは通過可能である
接触しているノードはclosedリストに含まれていない
4.currentに接触しているノードの g と h を計算し以下のルールを従う。
ルール①
もし、そのノードのg,h,p値がまだ設定されていない場合、そのノードのgとhを設定しそのノードのpをcurrentと設定する。
ルール②
もし、そのノードのg,h,p値が既に設定されている場合、新しく計算したgは既に設定されているgより少ない場合のみ新しく計算したgを設定し、そのノードのpをcurrentに設定する。
5.currentをclosedリストに追加する。
6.openリストの中で、g+hが一番低いノードをcurrentと設定する。
7.ステップ2からステップ7まで繰り返す。
実例
上記の手順だけではわかりにくいので、実際の例で上記の手順を使って一番短い道を見つけましょう。
まず、A出発地を「current」と定義する。

次、currentと接触しているノードをopenリストに追加する。
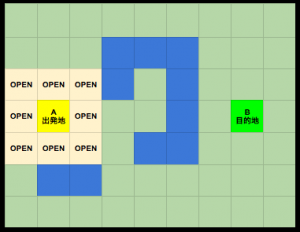
次、それぞれの g と h 値を計算し設定する。
なお、それぞれのpはcurrentとなります。
以下の図では、pを矢印で表す。
(それぞれのノードのpノードは差し先です)
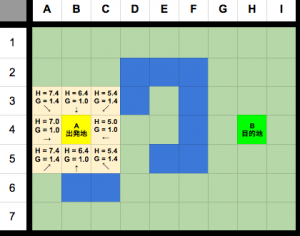
一旦、図を見てみましょう。
例として、C3にあるノードを見てみましょう。
C3のG値は1.4 出発地からC3まで、1.4m分の道を行かなければならないからです。
C3のH値は5.4 C3から目的地まで直線でいけたら、5.4mはまだあるからです。
(4つ右、1つ斜めので、4*1.0m + 1*1.4m = 5.4m)
なお、C3のpはまだ設定されていなかったので、pはcurrentのB4と設定されました。(左下向きの矢印で表している)
次はステップ5とステップ6。
current(B4)をclosedに追加し、openリストの中のgとhの合算が一番低いノードは新しいcurrentになります。
今の時点では、それはC4となります。
(C4の gとhの合算(5.0+1.0)は他のopenノードよりも低いため)
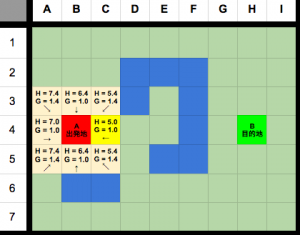
次はcurrent (C4)に接触しているノードをopenに追加する。
(ご注意:B4はclosedに含まれていて、D3は通過不可能ので、いずれも追加しない)
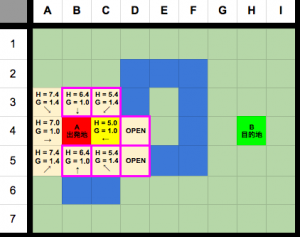
次、上記の図で紫枠になっているノードの g と hを計算します。
D4とD5は何も入っていないので入れるだけで問題ないですが、既に設定されているものも確認しなければなりません。
例として、C5を見てみましょう。
C5がB4から直接来た場合、gは1.4mになりますが、C4から来た場合2.0mになります
(B4→C4の1.om + C4→C5の1.0m)
既に設定された1.4mの方が短い道なので、C5のp(手前のノード)は出発地のB4のままでいいです。
なお、gを上書きしません。
計算が全部終わると、このようになります。
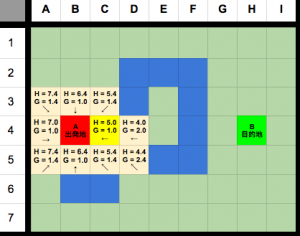
次はステップ5とステップ6。
確認済みのノードをclosedに追加して、g+hが一番低いノードをcurrentとして設定する。
gとhの合算が一番低いノードはD4です。
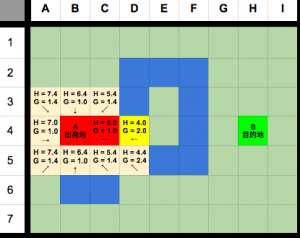
次はD4と接触しているノードをopenに追加し、gとhを計算する。
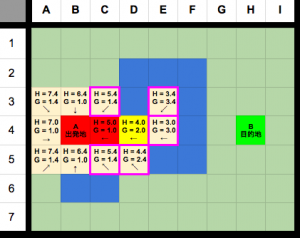
ご覧の通りE3,E4は設定されていなかったので設定されて、pがcurrentのD4となりました。
しかし、D4経由でC3,D5,C5まで行くとそれぞれのg値がより高くなってしまうので上書きされません。
(例えば、D4からD5に行く場合、gは3.0mになるが、C4からD5に行く場合、gは2.4mので、D5のpはC4のままでいいです)
次、各openノードを比較してgとhの合算が一番低いノード(E4)をcurrentにしD4をclosedリストに移す。
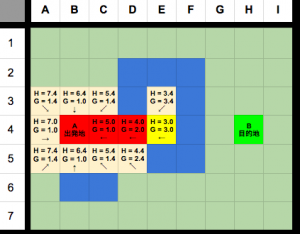
次は、E4と接触しているノードをopenして、gとhを計算する。
(今回、接触ノードは全て通過不可能、または既にopenに追加されているので、openリストに何も追加しなくていいが、E3とD5のE4から辿った場合のgを計算する必要があります。今回、どれも上書きされません。)
E4をclosedにし、gとhの合算が一番低いノードをcurrentに切り替える
しかし各openノードのgとhの合算を確認したら、E4もD5もC3もC5も同じ6.8mとなっています。
その場合、どちらを選んでも問題ないです。
今回の実例では、h値が一番低いものを優先に調べることにしましょう。
(結果的に、A*は一番短い道を確実に見つけてくれるけど、複数の等しい道がある場合、この「どれを優先に調べる」ルールはその等しい道の中、どの道になるかを影響する。優先順位をランダムで決定することでも問題ありません。)
E4、D5、C3、C5の中、
h値が一番低いのはE3ので、それをcurrentにします。
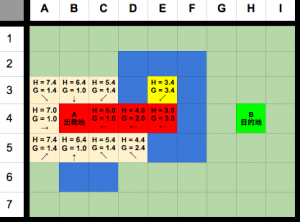
E3の接触ノードは全て通過不可能、またはclosedに入っている。
残念ながら、行き止まりでした。
g、hを計算できる接触ノードはありませんので、openリストを広げるステップをスキップし、E3をclosedに入れる。
まだC3,C5,D5、三つとも、6.8mとなっていますが、h値が低いのはD5ので、
それをcurrentに切り替える
そのD5の接触ノードを確認して、gとhの計算をする。
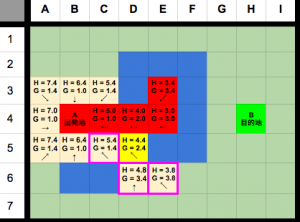
この手順を繰り返すと目的地に近づいていきます。
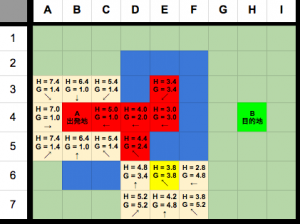
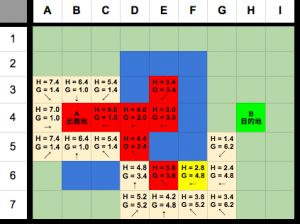
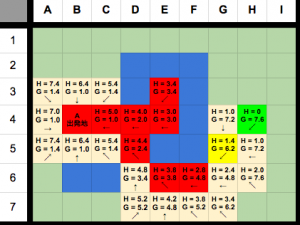
やっと、目的地のH4はopenリストに追加され、gとhが計算されました。
次のステップで目的地がcurrentになります。
そうなるとこの手順の繰り返しを完了します。
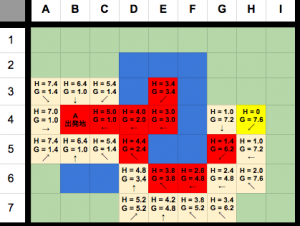
ちなみに目的地に着かずopenリストを尽くしてしまう場合もあります。
その場合「道が存在しない」という意味になるのでコードを書く時は、その可能性も考え対応する必要があります。
やっと目的地に辿り着いて一番短い道の距離は7.8mであることがわかりました。
目的地からp値で遡ると道のルートも取得できます。
目的地H4のpはG5.
G5のpはF6.
F6のpはE6.
E6のpはD5.
D5のpはC4.
C4のpは出発地のB4.
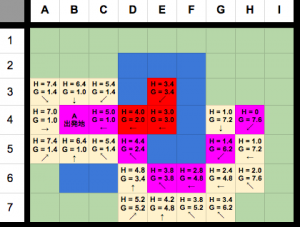
つまり、行く道はその反対
B4→C4→D5→E6→F6→G5→H4
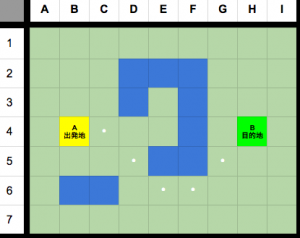
A* パスファインディングの特徴
上記の実例はとても単純なマップでしたが、複雑な迷路のようなマップでも1番短い道を必ず見つけてくれることが確実です。
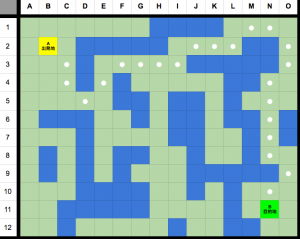
なおgとhの合算が低いものから調べていくため、他のパスファインディング方式より処理がより速いです。
ウェイティング(重み付け)
なお、ウェイティングをすると、通過可能の障害物もシミュレートできます。
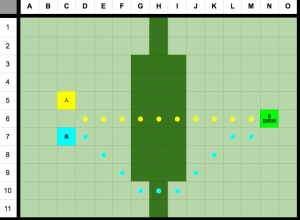
以下のマップを見てみましょう。
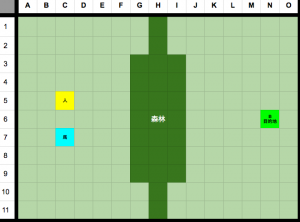
この実例では人と馬が目的地に行きたいですが、間に森林がある。
このゲームでは人は構いなく森林を通ることができるけど、馬は森林を避ける傾向を持つ(でも、仕方がない場合、通る)。
それをシミュレートするには、gを計算するとき何らかの重み付けを使います。
つまり、人がまっすぐ森林のノードに移ると+1.0と計算するが、
馬の場合、野原は森林より5倍好ましければ馬がまっすぐ森林のノードに移ると+5.0と計算する。
(hは通常通り、直線距離で計算する)
これをすると、人は割りとまっすぐなパスを辿る。
馬はできるだけ分厚い森林を避けようとする。
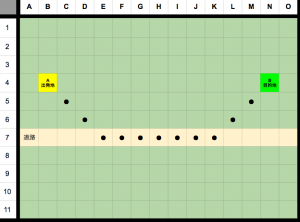
同様に、反対のこともできます。
「障害物」を避けるために重み付けをするだけではなく道路などを優先的に使うよう野原に重み付けをして、道路に重付けをしないこともできる。
***ご注意
重み付けをする際、1.0より小さい数字を使うと「必ず一番短い道を見つける」特徴がなくなります。
その反面大きいな数字を使うとあまりにも避けようとしすぎてコードの処理が遅くなります。
まとめ
『もしアップルパイを最初から作りたいと思ったら、まずは宇宙を創造しなければなりません』- Carl Sagan
マップ上で駒を動かすのはものすごく単純な行為には見えますが、プログラミングの世界では単純なことは中々ありません。
コンピュータにとっては簡単ですが、私は 312198 * 1912 の暗算はできません。
その反面、散歩をするときは自然に目的地まで歩くことができるのに、コンピュータにとっては自然ではないので、A*などの方式でコードを書いて教えなければなりません。
今回の記事で紹介しました方式は主に、ゲーム・プログラミングやロボティクスで活用できますが、このような問題を1つ1つ解決していくことがプログラマーの1番の楽しみと思います。
自分に挑戦したいと思う方は、ぜひ上記のA*パスファインディング方式を実際に使って簡単なプログラムでも書いてみるのはいかがでしょう。
